Support Vector Machine Chinese Version

Please note this post is a study note translated to Chinese by me. Click here to see the original English version in Wei’s homepage.

请注意: 本文是我翻译的一份学习资料，英文原版请点击Wei的学习笔记。

---

支持向量机

许多人认为支持向量机（SVM）是目前最好的分类器之一，也很容易在许多编程语言（如Python和Matlab）中实现。我将在这篇博客中讨论支持向量机的原理。另外，SVM中核函数的运用也允许了我们在高维度数据空间中应用SVM，因此核函数也会作为其中一个要点在文章中进行讨论。

1 直观理解与符号应用

通常，由于二元分类是多元分类中的最简单的情况，人们总是习惯从二元分类下手研究问题。关于二元分类，我们已经在先前的笔记中学过了一些概率模型，例如逻辑回归。至于SVM，它可以对随机空间维度中的点进行分类，并且可以通过使用确定性算法来解决问题。

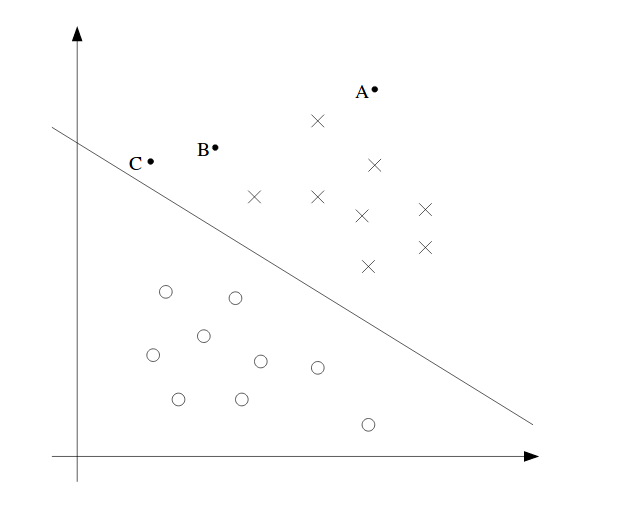
上述2D模型是一个简单的例子。从图中我们可以看到，在空间中有A，B和C点。A是最安全的点，因为它远离边界线（高维的超平面），而C是最危险的点，因为它接近超平面。边界线和点之间的距离称为间隔（margin）。

我们以$x$表示特征向量，以$y$表示分类结果，以$h$表示分类器。因此，SVM分类器可以表示为：

$$h_{w,b}(x) = g(w^Tx + b)$$

请注意，SVM和逻辑算法并不一样。在SVM中，w，b代替了原本的$\theta$，而且y的分类结果取值为1和-1，而不是0和1。分类器直接预测结果1或-1，而不像逻辑算法那样计算出概率，这点和感知器算法是一样的。 不过，一些库如Python中的scikit-learn，确实为SVM提供了概率输出。这是通过使用诸如逻辑函数之类的转换函数来实现的。

2 函数间隔与几何间隔

函数间隔关于训练数据的表达:

$$\overset{\wedge}{\gamma^{(i)}} = y^{(i)}(w^Tx^{(i)} + b)$$

当分类y为正数1时，我们希望$(w^Tx^{(i)} + b)$是一个较大的正数，当分类为负数-1时，则希望它是一个较大的负数。因此，这意味着函数间隔必须是正数才对。间隔越大，我们就分类的结果越自信。但是当我们将w和b的比例放大到2w和2b而不改变其他任何东西时，这可能并没有什么意义。虽然我们没有因此改变$(w^Tx^{(i)} + b)$的正负符号（也就是预测结果），但我们通过缩放w和b得到了更大的间隔。因此，为了使预测不因w和b的缩放倍数变动而变动，我们接下来将带来一个新的定义 - 几何间隔。此外，我们将数据集的函数间隔表示为：

$$\overset{\wedge}{\gamma} = \min_{i=1,\dots,m} \overset{\wedge}{\gamma^{(i)}}$$

其中，m为训练样本的数量。

几何间隔：在几何间隔中，我们认为w和b的缩放倍数大小不应影响间隔的比例，因此需要对w和b进行关于w范数的归一化。一个几何间隔的表示可见下图：

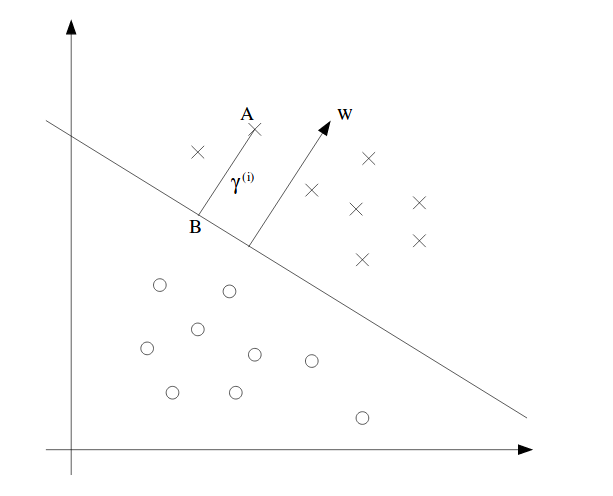
图中w也可以被称为支持向量。w与边界线相垂直，为了证明这一点，让我们在边界线上任取两点$x_i,x_j,i\neq j$。根据定义，我们有:

$$w^T x_i + b = w^T x_j + b = 0$$

于是，我们可以有:

$$w^T(x_i-x_j) = 0$$

$x_i-x_j$是沿着边界线的向量。我们知道如果两个向量的点积为零，那么这两个向量是相互垂直的。所以$w^T$与$(x_i-x_j)$互相垂直。

类似地，为了找到A点的间隔，我们声明$\gamma^{(i)}$为一个标量，我们将B点作为A点到边界线的投影点。根据定义，A点到B点可以表示为：$x^{(i)} - \gamma^{(i)} w/\lvert\lvert w \rvert\rvert$。如果这个点是在边界线上的话，可以表示为：

$$w^T(x^{(i)} - \gamma^{(i)} \frac{w}{\lvert\lvert w \rvert\rvert}) + b = 0$$

解：

$$\gamma^{(i)} = (\frac{w}{\lvert\lvert w \rvert\rvert})^T x^{(i)} + b/\lvert\lvert w \rvert\rvert$$

当然，这仅仅是结果（间隔）为正数的情况。对于负值样本，我们会得到一个负数的结果。所以为了统一这一点，我们将上面推演出的间隔乘以分类y（1或-1）。因此，我们将对于一个训练样本的几何间隔定义为：

$$\gamma^{(i)} = y^{(i)}((\frac{w}{\lvert\lvert w \rvert\rvert})^T x^{(i)} + b/\lvert\lvert w \rvert\rvert)$$

如果$\lvert\lvert w \rvert\rvert = 1$，函数间隔则等于几何间隔。几何间隔不会随着w和b的倍数变化而变化，这意味着如果我们将w和b放大2倍，我们将具有相同的几何间隔（不是函数间隔）。这里请注意，我们必须使用相同的标量来缩放两个参数。那么关键点来了，这种情况下，我们想要任何的函数间隔都可以，同时我们仍然可以拥有相同的几何间隔。

类似地，对于所有训练样本的几何间隔是：

$$\gamma = \min_{i=1,\dots,m}\gamma^{(i)}$$

3 最优间隔分类器（OMC）

最重要的是，简单来说，我们的目标是最大化几何间隔，越大越好。

目前，我们假设数据是线性可分的。这个优化问题可以定义为：

$$\begin{align} \max_{\gamma,w,b} & \gamma \\ \text{s.t. } & y^{(i)}(w^Tx^{(i)} + b) \geq \gamma, i = 1,\dots,m \\ & \lvert\lvert w \rvert\rvert = 1 \end{align}$$

第一个约束是确保每个训练样本都具有有效的几何间隔。第二点是为了确保几何间隔等于函数间隔。我们必须有第二个约束，因为$y^{(i)}(w^Tx^{(i)} + b)$是函数间隔。通过第二个约束，我们使得函数间隔等于几何间隔。令人很难受的点是第二个约束$\lvert\lvert w \rvert\rvert = 1$，使得它不是凸的。如果它是凸的，我们可以对它求导并设它为零来找到极值，但这是另一个话题了。

为此，我们可以将其转换为：

$$\begin{align} \max_{\overset{\wedge}{\gamma},w,b} & \frac{\overset{\wedge}{\gamma}}{\lvert\lvert w \rvert\rvert} \\ \text{s.t. } & y^{(i)}(w^Tx^{(i)} + b) \geq \overset{\wedge}{\gamma}, i = 1,\dots,m \end{align}$$

我们使用了函数间隔来表示几何间隔。这里我们用了最初预期的函数间隔，而不是几何间隔。 通过这样做，我们消除了$\lvert\lvert w \rvert\rvert = 1$。但这仍然很糟糕。

回想一下，通过缩放w和b，我们没有改变任何东西。我们使用这个事实来强制函数间隔$\overset{\wedge}{\gamma} = 1$，而不改变几何间隔。之后，我们的最大值问题现在可以表示为最小值问题：

$$\begin{align} \min_{\gamma,w,b} & \frac{1}{2} \lvert\lvert w \rvert\rvert^2 \\ \text{s.t. } & y^{(i)}(w^Tx^{(i)} + b) \geq 1, i = 1,\dots,m \end{align}$$

同样，我们有$\frac{1}{2}$的原因只是为了数学计算上方便，这并不会制造出任何问题。现在，这个问题已经可以通过使用二次规划软件来解决了，不过我们仍然可以进一步简化这一过程，进一步的简化需要了解拉格朗日对偶性

4 拉格朗日对偶性

关于如何解决约束优化问题，让我们稍稍插入另一个话题。一般来说，我们通常使用拉格朗日对偶来解决这类问题。

我们考虑这样一个问题:

$$\begin{align} \min_w & f(w) \\ \text{s.t. } & h_i(w) = 0,i = 1,\dots,l \end{align}$$

现在，我们可以将拉格朗日定义为：

$$\mathcal{L}(w,\beta) = f(w) + \sum\limits_{i=1}^l \beta_i h_i(w)$$

其中$\beta_i$称为拉格朗日乘数。现在，我们可以求偏导数并设为零，并找出每个$w_i$和每个$\beta_i$。

上述只有等式约束，同时我们可以推演到等式和不等式约束。所以我们定义Primal Problem为：

$$\begin{align} \min_w & f(w) \\ \text{s.t. } & g_i(w) \leq 0,i = 1,\dots,k \\ & h_i(w) = 0,i = 1,\dots,l \end{align}$$

我们将广义拉格朗日定义为:

$$\mathcal{L} = f(w) + \sum\limits_{i=1}^k \alpha_i g_i(w) + \sum\limits_{i=1}^l \beta_i h_i(w)$$

其中所有的$\alpha$和$\beta$都是拉格朗日乘子。

让我们定义primal problem的数量为:

$$\theta_{\mathcal{P}}(w) = \max_{\alpha,\beta:\alpha_i\geq 0} \mathcal{L}(w,\alpha,\beta)$$

在这个数量中，我们需要$\alpha_i$大于零。如果$\alpha_i < 0$，则由于$g_i(w) \leq 0$，则上述量的最大值就是$\infty$。此外，如果违反了某些约束，那么我们也将得到$\theta_{\mathcal{P}}(w) = \infty$。

如果所有条件都满足的话，我们将有：

$$\theta_{\mathcal{P}}(w) = \begin{cases} f(w) \text{, if w 满足 primal 约束} \\ \infty \text{, 其他情况} \\ \end{cases}$$

为了与我们的primal problem相匹配，我们将最小问题定义为：

$$\min_w \theta_{\mathcal{P}}(w) = \min_w \max_{\alpha,\beta:\alpha_i\geq 0} \mathcal{L}(w,\alpha,\beta)$$

如果满足了所有约束，那么这将与primal problem相同。我们将primal problem的值定义为：$p^{\ast} = \min_w \theta_{\mathcal{P}(w)}$

从不同的角度我们可以将以下定义为dual problem（对偶问题）的一部分：

$$\theta_{\mathcal{D}}(\alpha,\beta) = \min_w \mathcal{L}(w,\alpha,\beta)$$

为了再次与primal problem相匹配，我们将对偶最优化问题(dual optimization problem)定义为：

$$\max_{\beta,\alpha:\alpha_i\geq 0} \theta_{\mathcal{D}}(\alpha,\beta) = \max_{\alpha,\beta:\alpha_i\geq 0} \min_w \mathcal{L}(w,\alpha,\beta)$$

相同的，对偶问题的值为：$d^{\ast} = \max_{\alpha,\beta:\alpha_i\geq 0} \theta_{\mathcal{D}}(\alpha,\beta)$

Primal 和 dual problem 的相关性为:

$$d^{\ast} = \max_{\alpha,\beta:\alpha_i\geq 0} \theta_{\mathcal{D}}(\alpha,\beta) \leq p^{\ast} = \min_w \theta_{\mathcal{P}(w)}$$

上述公式永远为真。要证明这一点，我们首先定义一个函数$f(x,y): X \times Y \mapsto \mathbb{R}$。然后，我们可以定义:

$$g(x) := \min_{y} f(x,y)$$

也就是说，对于函数g的每个x，我们选一个能使f（x，y）最小化的y值。然后，我们可以说：

$$g(x) \leq f(x,y) \forall x\forall y$$

我们可以在两边各添加一个max运算符，以消除变量x：

$$\max_{x} g(x) \leq \max_{x} f(x,y) \forall y$$

这等同于:

$$\max_{x} \min_{y} f(x,y) \leq \min_{y} \max_{x} f(x,y)$$

以上便是证明的过程。

回到主题：关键是在某些条件下，它们是相等的。如果他们是相等的，我们可以专注于dual problem而不是primal problem。那么唯一的问题将是 - 它们何时相等。

我们假设f和g都是凸函数，h是仿射函数（当f有Hessian时，如果Hessian是正半正定则它是凸的。所有仿射都是凸的，仿射意味着线性。），对于一些w，函数g全部小于0。

从这些假设出发，primal的解$w^{\ast}$一定存在，dual的解$\alpha^{\ast},\beta^{\ast}$一定存在，同时$p^{\ast} = d^{\ast}$，并且$w^{\ast}$，$\alpha^{\ast}$和$\beta^{\ast}$满足 Karush-Kuhn-Tucker（KKT）条件，KKT条件是：

$$\frac{\partial}{\partial w_i}\mathcal{L}(w^{\ast},\alpha^{\ast},\beta_{\ast}) = 0. i = 1,\dots,n$$ $$\frac{\partial}{\partial \beta_i}\mathcal{L}(w^{\ast},\alpha^{\ast},\beta_{\ast}) = 0. i = 1,\dots,l$$ $$\alpha_i^{\ast}g_i(w^{\ast}) = 0,i = 1,\dots,k$$ $$g_i(w^{\ast}) \leq 0,i = 1,\dots,k$$ $$\alpha_i^{\ast} \geq 0,i = 1,\dots,k$$

第三个等式被称为KKT dual complementarity condition。意思是如果$\alpha_i^{\ast} > 0$，那么$g_i(w^{\ast}) = 0$。当primal problem等于dual problem时，上述的每个条件和假设都会成立。

5 OMC与拉格朗日对偶性

让我们回到SVM的primal problem：

$$\begin{align} \min_{\gamma,w,b} & \frac{1}{2} \lvert\lvert w \rvert\rvert^2 \\ \text{s.t. } & y^{(i)}(w^Tx^{(i)} + b) \geq 1, i = 1,\dots,m \end{align}$$

我们可以重新设定约束为：

$$g_i(w) = -y^{(i)}(w^Tx^{(i)} + b) + 1 \leq 0$$

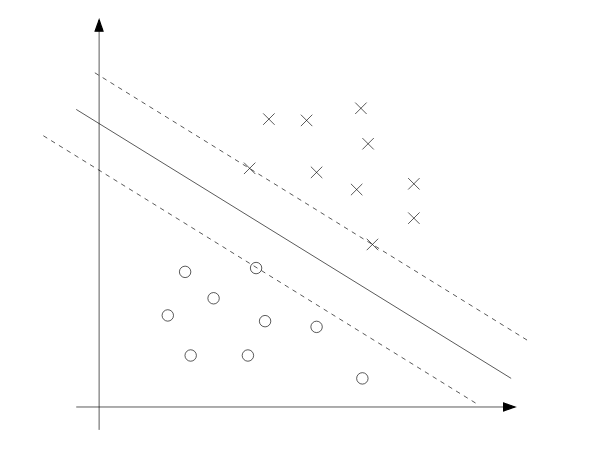
其中i包含所有训练样本。从KKT条件中我们可以看到，当函数间隔为1且$g_i(w) = 0$时，$\alpha_i > 0$。

我们可以在下面的图片中看到这一点:虚线上的三个点是具有最小几何间隔的点，所以这些点的$\alpha_i$为正值。这些点也被称为支持向量。

仅有不等式约束的拉格朗日：

$$\mathcal{L}(w,b,\alpha) = \frac{1}{2}\lvert \lvert w\rvert \rvert^2 - \sum\limits_{i=1}^m \alpha_i [y^{(i)}(w^Tx^{(i)} + b) - 1] \tag{1}$$

要找到这个问题的对偶形式（dual form）的话，我们需要在给定$\alpha$的情况下，找到损失函数中w和b的最小值：

对于 w：

$$\triangledown_{w}\mathcal{L}(w,b,\alpha) = w - \sum\limits_{i=1}^m \alpha_i y^{(i)}x^{(i)} = 0\tag{2}$$

这说明： $w = \sum\limits_{i=1}^m \alpha_i y^{(i)}x^{(i)}\tag{3}$

对于 b：

$$\frac{\partial}{\partial b}\mathcal{L}(w,b,\alpha) = \sum\limits_{i=1}^m \alpha_i y^{(i)} = 0 \tag{4}$$

一个有用的公式:

$$\begin{align} \lvert\lvert\sum\limits_{i=1}^m \alpha_i y^{(i)}x^{(i)}\rvert\rvert^2 &= (\sum\limits_{i=1}^m \alpha_i y^{(i)}x^{(i)})^T(\sum\limits_{i=1}^m \alpha_i y^{(i)}x^{(i)}) \\ &= \sum\limits_{i,j}^m y^{(i)}y^{(j)}\alpha_i\alpha_j (x^{(i)})^Tx^{(j)} \end{align}$$

我们将等式（3）带回到等式（1），得到：

$$\begin{align} \mathcal{L}(w,b,\alpha) &= \frac{1}{2}\sum\limits_{i,j}^m y^{(i)}y^{(j)}\alpha_i\alpha_j (x^{(i)})^Tx^{(j)} \\ & - \sum\limits_{i=1}^m \alpha_i [y^{(i)}((\sum\limits_{j=1}^m \alpha_j y^{(j)}x^{(j)})^Tx^{(i)} + b) - 1] \\ &= \frac{1}{2}\sum\limits_{i,j}^m y^{(i)}y^{(j)}\alpha_i\alpha_j (x^{(i)})^Tx^{(j)} - \sum\limits_{i,j}^m y^{(i)}y^{(j)}\alpha_i\alpha_j (x^{(i)})^Tx^{(j)} \\ & - b\sum\limits_{i=1}^m\alpha_i y^{(i)} + \sum\limits_{i=1}^m \alpha_i \\ &= \sum\limits_{i=1}^m \alpha_i - \frac{1}{2}\sum\limits_{i,j}^m y^{(i)}y^{(j)}\alpha_i\alpha_j (x^{(i)})^Tx^{(j)} \end{align}$$

我们需要注意$\alpha_i \geq 0$ 和约束（4）。因此，我们得到的dual problem为：

$$\begin{align} \max_{\alpha} W(\alpha) &= \sum\limits_{i=1}^m \alpha_i - \frac{1}{2}\sum\limits_{i,j}^m y^{(i)}y^{(j)}\alpha_i\alpha_j <x^{(i)},x^{(j)}> \\ \text{s.t. } & \alpha_i \geq 0, i = 1,\dots,m \\ & \sum\limits_{i=1}^m \alpha_i y^{(i)} = 0 \end{align}$$

这是满足KKT条件的，可以自己尝试着去证明一下。这意味着我们现在要解决的是dual problem而不是primal problem。如果我们可以在这个dual problem中找到$\alpha$，我们就可以用等式（3）去找到$w^{\ast}$。有了最优化的$w^{\ast}$，我们可以找到$b^{\ast}$：

$$b^{\ast} = -\frac{\max_{i:y^{(i)}=-1}w^{\ast T}x^{(i)} + \min_{i:y^{(i)}=1}w^{\ast T}x^{(i)}}{2}$$

想验证它的话很容易。基本上我们要做的就是，分别从正负两个类别中取出与超平面具有相同距离的点，也就是支持向量。由于它们的间隔是相同的，我们可以很好的用这个属性来解$b^{\ast}$。将w和b最优化后，最近的正负样本的几何间隔将会相等。

等式（3）所表达的是：最优化的w是基于最优化的$\alpha$的。为了做出预测，我们可以：

$$w^Tx + b = (\sum\limits_{i=1}^m \alpha_i y^{(i)} x^{(i)})^Tx + b = \sum\limits_{i=1}^m \alpha_i y^{(i)} <x^{(i)},x> + b$$

如果大于零，我们预测1，小于零则预测-1。我们知道，由于约束，除了支持向量以外的所有$\alpha$将为零。这意味着我们只关心x与支持向量的内积。这使得预测更快并且将核函数概念带入我们的讨论中。请记住，到目前为止，一切都是低维度的。那么高维度和无限维度空间将会是什么情况呢？

6 核函数

在房屋居住区域的例子中，我们可以使用特征$x,x^2,x^3$来获得三维函数，其中$x$可以是房屋的大小。 我们称$x$为输入属性，$x,x^2,x^3$，称为特征。我们声明一个特征映射函数$\phi (x)$，这个函数可以将输入属性映射到特征。

因此，我们可以在新的特征空间$\phi (x)$中进行训练学习。在上一节结尾我们了解了，需要计算内积$<x,z>$。现在我们可以用$<\phi(x),\phi(z)>$替换它。

定义上讲，给定一个映射函数我们可以将核函数声明为：

$$K(x,z) = \phi(x)^T\phi(z)$$

这里我们可以使用核函数，而不是映射函数本身，其原因可以在cs229课程的原笔记中找到，由于内容比较细节这里就不再过多赘述。简而言之，核函数在计算上复杂度较低，并且可以用于高维度或无限维度映射中。所以我们可以在高维空间中进行训练而无需计算映射函数$\phi$。

原笔记中有一个例子证明了核函数的效率之高。你需要知道的是，计算映射所需要的时间复杂度是呈指数的，而计算核函数需要的时间复杂度是线性的。

换句话说，核函数是用来计算两个样本（x 和 z）之间的远近的，它呈现了相似性的概念。在流行的核函数中，有一个被称为高斯核函数，其定义如下：

$$K(x,z) = \exp(-\frac{\lvert\lvert x-z \rvert\rvert^2}{2\sigma^2})$$

我们可以使用它来训练SVM，它对应的是无限维度特征映射函数$\phi$。这意味着映射函数$\phi$是无限维度的。计算机是无法计算无线维度上的映射函数的，但我们可以使用核函数来直接得出对于应的內积值。

接下来，我很想讨论下关于核函数有效性的事情。

我们定义拥有m个点的核矩阵为$K_{ij} = K(x^{(i)},x^{(j)})$ K是 m x m 矩阵。那么现在，如果K是有效的话，这意味着：

(1)对称矩阵: $K_{ij} = K(x^{(i)},x^{(j)}) = \phi(x^{(i)})^T\phi(x^{(j)}) = \phi(x^{(j)})^T\phi(x^{(i)}) = K_{ji}$

(2)半正定矩阵: $z^TKz \geq 0$ 这个证明很简单，如果需要的话可以提供过程。

Mercer定理（Mercer Theorem的中文无对应翻译）：设$K:\mathbb{R}^n \times \mathbb{R}^n \mapsto \mathbb{R}$。为了使核函数有效，对于任何${x^{(1)},\dots,x^{(m)}}$，对应的核矩阵必须同时是对称的，也是半正定的，这是一个充要条件。

核函数方法不仅在SVM中有运用，它在任何有内积的情况下都是用途颇广的。因此，我们用核函数替换内积，以便在更高的维度空间中使用。

7 正规化与无法分割问题

尽管将x映射到更高维度的空间增加了可分离的机会，但情况可能并非总是如此。一个异常值的出现也是非常棘手的，我们不会想把这种异常值放入训练集的。下图演示了这种情况：

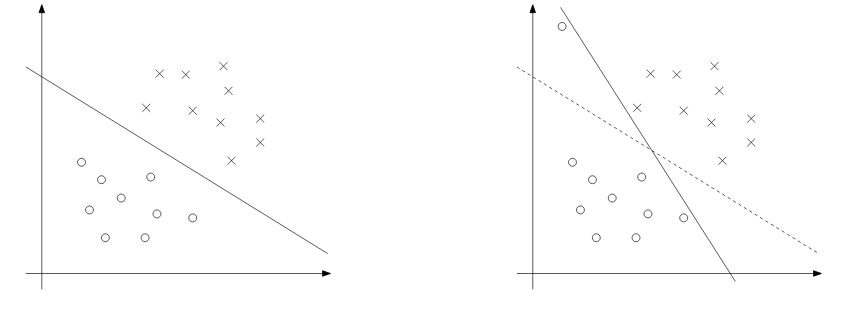
为了使算法也适用于非线性情况，我们将用到正则化：

$$\begin{align} \min_{\gamma,w,b} & \frac{1}{2}\lvert\lvert w\rvert\rvert^2 + C\sum\limits_{i=1}^m \xi_i \\ \text{s.t. } & y^{(i)}(w^Tx^{(i)} + b) \geq 1-\xi_i,i=1,\dots,m \\ & \xi_i \geq 0,i=1,\dots,m \end{align}$$

正规化将惩罚对于函数间隔小于1的样本，C将确保大多数样本的函数间隔至少为1。这表明了：

(1) 我们希望w小，这样间隔就会大。

(2) 我们希望大多数样本的函数间隔大于1。

拉格朗日为：

$$\begin{align} \mathcal{L}(w,b,\xi,\alpha,r) &= \frac{1}{2}w^Tw + C\sum\limits_{i=1}^{m}\xi_i \\ & - \sum\limits_{i=1}^m \alpha_i[y^{(i)}(x^{(i)T}w + b) - 1 + \xi_i] - \sum\limits_{i=1}^{m}r_i\xi_i \end{align}$$

其中$\alpha$和r是拉格朗日乘数。因为这里的约束是不等式约束，所以这些乘数不能是负数。现在，我们需要做同样的事情来找出dual problem的形式，这里的过程我也不再赘述了。在将w和b的导数设为零之后，带回后得到dual problem：

$$\max_{\alpha} W(\alpha) = \sum\limits_{i=1}^{m}\alpha_i - \frac{1}{2}\sum\limits_{i,j=1}^{m}y^{(i)}y^{(j)}\alpha_i\alpha_j<x^{(i)},x^{(j)}>$$ $$\text{s.t. }0\leq \alpha_i \leq C,i=1,\dots,m$$ $$\sum\limits_{i=1}^{m}\alpha_i y^{(i)} = 0$$

注意，$\alpha$的值有一个区间。这是因为$\sum\limits_{i=1}^{m}(C-\alpha_i-r_i)\xi_i$。我们将$\xi$取导并设零，将得到的结果带回原等式消除$\xi$，我们便得到了$\alpha$的区间。在这个情况下，当$r_i = 0$时，$r_i$始终为非负数，$\alpha_i=C$。

还需要注意的是，由于两个最近的点的间隔都已改变，这里的最优b不再与之前相同。在下一节中，我们将找到一个合适的算法来解决问题。

8 序列最小优化算法（SMO）

John Platt的SMO（顺序最小优化）算法的出现是用来解决SVM中的dual problem的。

8.1 坐标上升法

一般来讲，最优化问题

$$\max_{\alpha}W(\alpha_1,\alpha_2,\dots,\alpha_m)$$

可以通过梯度上升和牛顿法来解决。另外，我们也可以使用坐标上升法：

for loop until convergence:
  for i in range(1,m):
    alpha(i) = argmin of alpha(i) W(all alpha)

总的来说，我们将除$\alpha_i$之外的所有$\alpha$固定，然后移动到下一个$\alpha$进行更新。 假设计算$\alpha$的梯度是有效的。举个例子：

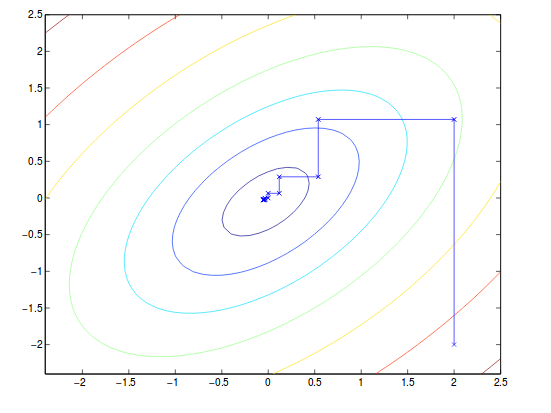
这里请注意，收敛的路径始终与x或y轴平行，因为它每一次只更新一个变量。

8.2 序列最小优化算法（SMO）

我们不能在SVM的dual problem中做与上面相似的事情，因为只改变一个变量可能会违反约束：

$$\alpha_1 y^{(1)} = -\sum\limits_{i=2}^m \alpha_i y^{(i)}$$

这表示一旦我们确定剩余部分的$\alpha$，我们就不能再改变左边的$\alpha$了。因此，我们必须一次性改变两个$\alpha$并更新它们。例如，我们可以：

$$\alpha_1 y^{(1)} + \alpha_2 y^{(2)} = -\sum\limits_{i=3}^m \alpha_i y^{(i)}$$

我们使右边保持不变:

$$\alpha_1 y^{(1)} + \alpha_2 y^{(2)} = \zeta$$

在图中可以表示为:

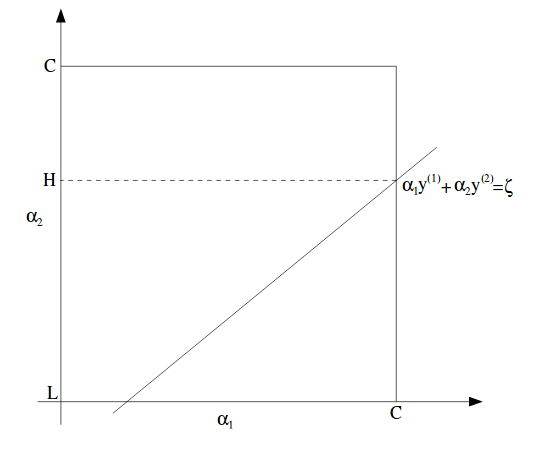
在此图中，L和H是$\alpha_2$可能达到的最低值和最高值，而$\alpha_1$介于0和C之间。

这里注意，尽管$\alpha$是在这个正方形中的，不过给定一条直线，它们的上下限会有所限制。

我们可以重写上面的等式：

$$\alpha_1 = (\zeta - \alpha_2 y^{(2)})y^{(1)}$$

那么W将会是:

$$W(\alpha_1,\dots,\alpha_m) = W((\zeta-\alpha_2 y^{(2)})y^{(1)},\alpha_2,\dots,\alpha_m)$$

我们将所有其他$\alpha$视为常量。因此，带入等式后W将变为二次函数，对于某些a，b和c，可以写为$a\alpha_2^2 + b\alpha_2 + c$。

最后，我们将$\alpha_2^{new, unclipped}$定义为用来更新$\alpha_2$的解决方案。因此，通过针对这一个变量应用约束，我们可以得到：

$$\alpha_2^{new} = \begin{cases} H \text{, if }\alpha_2^{new, unclipped}>H \\ \alpha_2^{new, unclipped} \text{, if } L\leq \alpha_2^{new, unclipped} \leq H \\ L \text{, if } \alpha_2^{new, unclipped} < L \\ \end{cases}$$